数独(Sudoku)は、9×9のグリッドに1から9までの数字を埋めていくパズルです。数独のルールはシンプルですが、解くためには論理的な思考が必要であり、非常に奥が深いパズルとして人気があります。

この記事では、Pythonを使って数独を解くアルゴリズムをステップごとに解説していきます。

もし、pythonの環境がない方は以下の記事で詳しく解説しているよ!
数独とは?
数独は、縦横9列、9行、さらに3×3のマス目に分かれたボード上に数字を配置するパズルです。以下のルールに従います。
- 各行に1から9までの数字を一度ずつ使用。
- 各列に1から9までの数字を一度ずつ使用。
- 各3×3のボックスにも1から9までの数字を一度ずつ使用。
解くためのアルゴリズム
数独を解くための典型的なアルゴリズムの一つに「バックトラッキング法」があります。バックトラッキングとは、解の候補を一つ一つ試し、矛盾が生じた場合に直前の状態に戻ってやり直す方法です。
バックトラッキングの流れ
バックトラッキングを使って数独を解くプロセスは次のようになります。
空いているマスを探す
数独のボード上で未入力のセルを見つける。
1から9までの数字を順番に試す
未入力のセルに1から9までの数字を入れてみる。
制約を満たすか確認
数字を入れた後、同じ行、列、3×3のボックス内で重複する数字がないか確認する。
矛盾がなければ次へ進む
問題がなければ次の空いているマスに移り、同じ操作を繰り返す。
矛盾が生じた場合は戻る
数字が矛盾する場合は、そのセルに別の数字を試す。全ての数字が試されて矛盾が解決できない場合は、一つ前のステップに戻り、再度数字を変更していく。
Pythonでの実装
実際にPythonで数独を解くプログラムを以下に示します。
# 数独の解法プログラム
def is_valid(board, row, col, num):
# 行、列、3x3のボックスに対してnumが有効かを確認
for i in range(9):
if board[row][i] == num or board[i][col] == num:
return False
box_row_start = (row // 3) * 3
box_col_start = (col // 3) * 3
for i in range(3):
for j in range(3):
if board[box_row_start + i][box_col_start + j] == num:
return False
return True
def find_empty(board):
# 空いているセルを探す。見つからない場合はNoneを返す
for i in range(9):
for j in range(9):
if board[i][j] == 0:
return i, j
return None
def solve_sudoku(board):
empty = find_empty(board)
if not empty:
return True # 空きがない場合は解決済み
row, col = empty
for num in range(1, 10):
if is_valid(board, row, col, num):
board[row][col] = num # 数字を仮置き
if solve_sudoku(board):
return True
board[row][col] = 0 # 元に戻す(バックトラッキング)
return False
# サンプルの数独問題(0は空きマスを表す)
sudoku_board = [
[5, 3, 0, 0, 7, 0, 0, 0, 0],
[6, 0, 0, 1, 9, 5, 0, 0, 0],
[0, 9, 8, 0, 0, 0, 0, 6, 0],
[8, 0, 0, 0, 6, 0, 0, 0, 3],
[4, 0, 0, 8, 0, 3, 0, 0, 1],
[7, 0, 0, 0, 2, 0, 0, 0, 6],
[0, 6, 0, 0, 0, 0, 2, 8, 0],
[0, 0, 0, 4, 1, 9, 0, 0, 5],
[0, 0, 0, 0, 8, 0, 0, 7, 9]
]
if solve_sudoku(sudoku_board):
for row in sudoku_board:
print(row)
else:
print("解けませんでした")
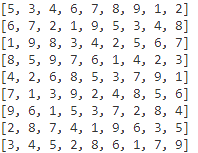
コードの解説
is_valid 関数
この関数は、指定された row 行、col 列に num を配置することが有効かどうかをチェックします。
行と列の確認:
まず、for ループを使って、row 行と col 列に num が既に存在していないか確認します。どちらかに同じ数字があれば False を返します。
3×3ボックスの確認:
数独は9×9のグリッドが3×3の小さなボックスに分かれています。そのため、指定されたセルが属する3×3のボックス内に num が既に存在しないかもチェックします。まず box_row_start と box_col_start でそのボックスの左上隅の座標を計算し、そこから3×3の範囲を調べます。
すべてのチェックをパスすれば True を返し、有効な配置だと判断します。
find_empty 関数
この関数は、数独のボードから空いている(まだ数字が埋められていない)セルを見つけ出します。
二重の for ループ:
外側の i ループが行を、内側の j ループが列をそれぞれ走査し、board[i][j] が 0(空のセルを意味する)であれば、その位置 (i, j) を返します。
セルが見つからない場合:
空いているセルが一つもなければ None を返し、ボードがすでに埋まっていることを示します。
solve_sudoku 関数
この関数は、バックトラッキングアルゴリズムを使って数独を解くメインのロジックです。
空いているセルを探す:
まず find_empty を呼び出して空いているセルを探します。空きがなければ、数独は解かれた状態なので True を返して終了します。
1から9までの数字を試す:
空きがあれば、そのセルに対して1から9までの数字を順に試します。各数字が is_valid 関数を通じて有効であれば、その数字を仮にボードに配置します。
再帰的な解決:
数字を配置したら、再び solve_sudoku を呼び出して次のステップに進みます。この再帰呼び出しは、ボード全体が解かれるまで繰り返されます。
バックトラッキング:
もし途中で問題が発生し、数独が解けない場合は solve_sudoku が False を返します。そのとき、仮に配置した数字を 0 に戻し、別の数字を試します。これを「バックトラッキング」と呼びます。
結論
数独を解くためのバックトラッキングアルゴリズムは、シンプルでありながら強力です。このアルゴリズムを実装することで、コンピュータを使ってさまざまな数独の問題を解くことができます。今回のPythonプログラムは基本的な数独の問題に対応していますが、他にもヒューリスティックや高速化のための工夫が考えられます。興味があれば、より高度な数独ソルバーに挑戦してみてください!

これで、Pythonで数独を解くアルゴリズムの基本的な実装が完成しました。ぜひ、自分で数独の問題を解いてみてください!




コメント